Segment Trees

Why do we need a segment tree?

Let's say we had an array that looked like this:

And we wanted to know what the sum of the values from indices 2 to 6 were. Easy, right? Just iterate through the list starting at index 2 and add up the numbers until you get to index 6.

What's the time complexity of this? You have to visit every element in between the two given indices. Because they could be anywhere from the start to the end of the list, it is O(n). That's not too bad for small lists like this, but what if we had a list of size 10,000 and we wanted to know the sum of the elements in the range of 5-9995? That's a lot of time we don't need to spend.

So how can we save time?

We could keep a second list that's the same size of the first one that keeps track of the ongoing sum from left to right. It would look like this for the above example:

Then, if we wanted to find the sum of the elements in the range from 2 to 6 in the original array, we take the element at index 6 in this new array and subtract it from the element right before index 2.

Look at that, so easy and it's done in two steps, which is O(1) time. We're done right? Nope. This is great if our original array never changes, but what if it does? Say we change the element at index 3 in our array to 30.

How does our sum list change? We have to recalculate all the values from index 3 on to account for the new value.

Dang. So with our first approach we could update values in O(1) time and calculate the range of a sum in O(n) time. With our second approach we can calculate the range of a sum in O(1) time but updating values takes O(n) time. Is there any way to strike a balance between the two?

What is a segment tree?

A segment tree of our array looks like this:

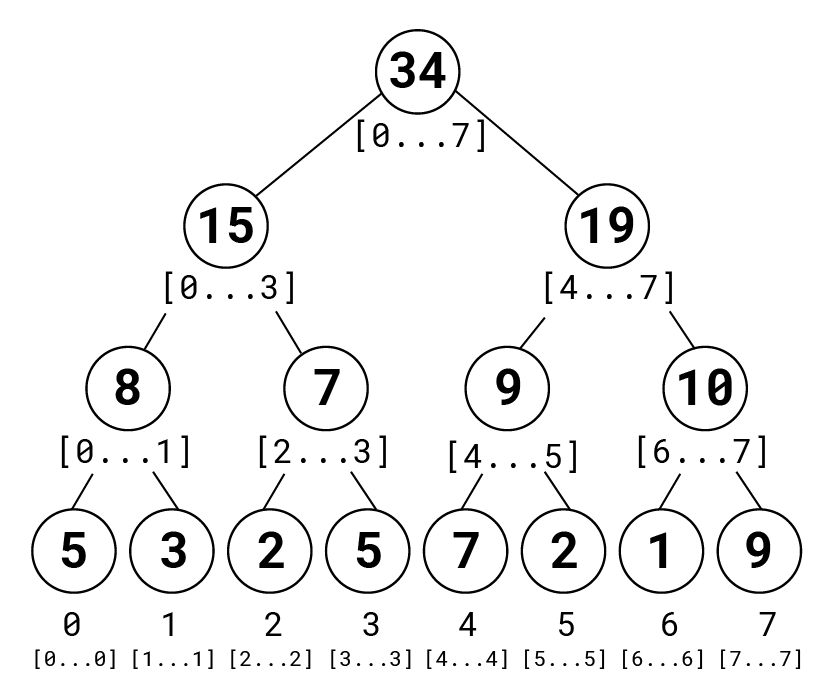
Each leaf node represents an element in our list, as well as an interval that consists of only the index that element is at. The first element represents the interval from 0 to 0, or [0...0], the second represents the interval [1...1] and so on. Then, we can build upward to an interval that represents the entire list. The node right above the first two represents the range [0...1] and consists of the sum of the elements from index 0 to 1. That is found easily by adding the value of the two nodes below it. We can do that for every pair of elements that are right next to each other, then repeat that process until we reach the top.

So how do we update a value?

Let's update the element at index 3 to 30 again. We traverse down the list to get to the leaf node that represents index 3, which is of value 5. We change that to 30, then begin to go back up.

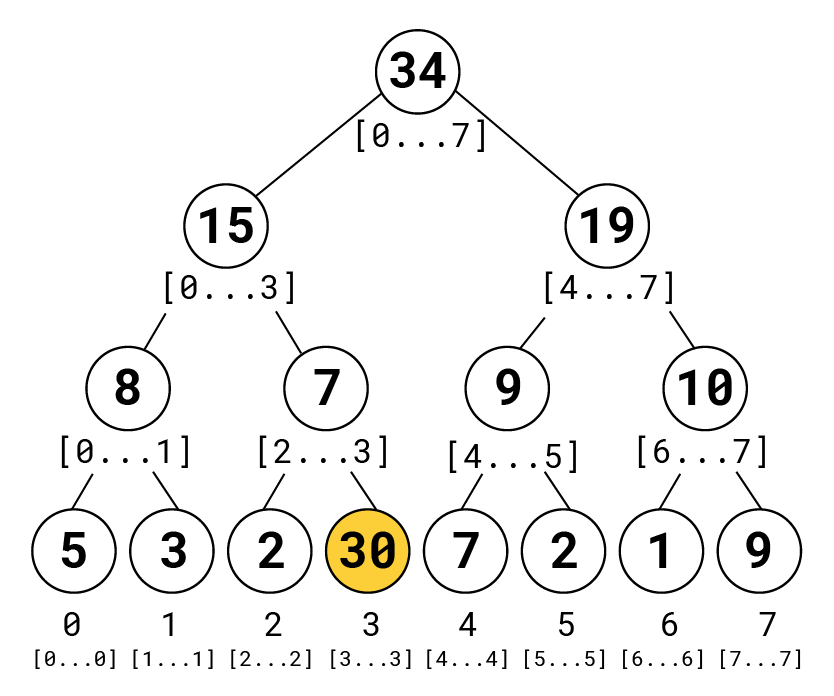
The interval [2..3] should now hold a different value. We set it to the sum of the two nodes below it:

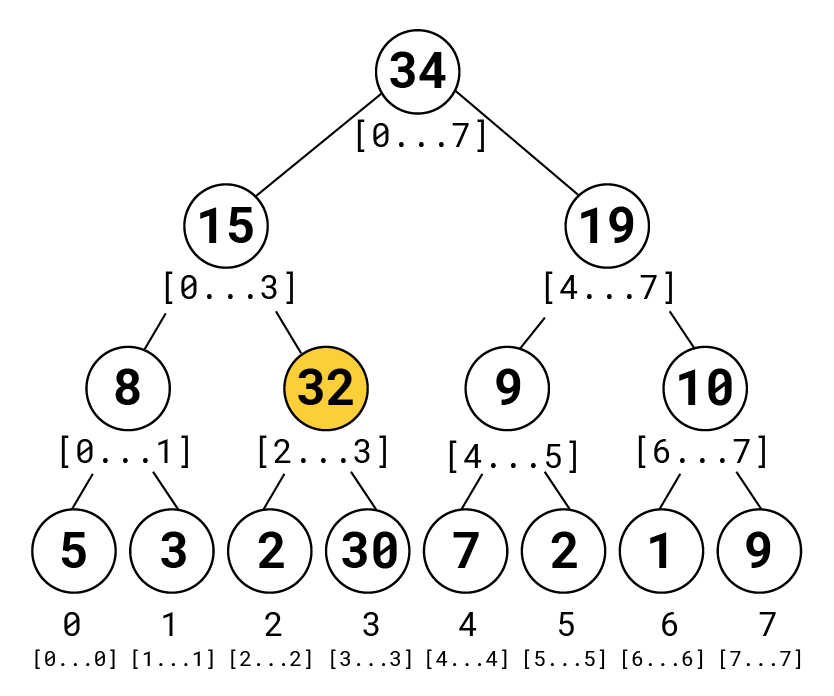
And we just keep going till the top:

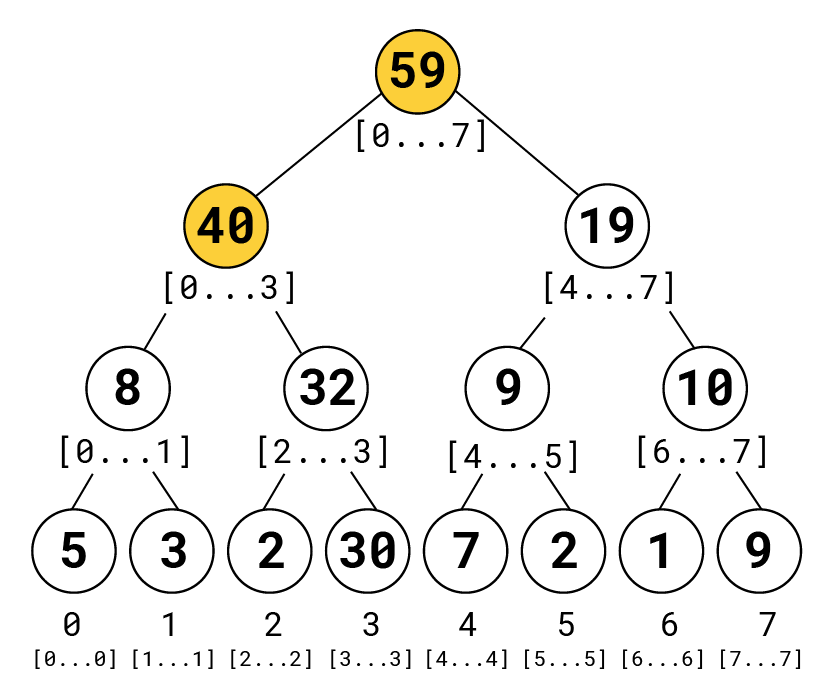
Great. As you can see, updating a single value takes O(log n) time. What about finding the sum of an interval?

Say we wanted to find the sum of the elements from indices 2 to 6 again. We start at the top of the tree and call a recursive algorithm that looks like this:

1. If there is no overlap, we return 0.
2. If any part of the interval of the node we are currently at is outside the range we are searching for, we call this function on its two children.
3. If the interval of the current node is inside (inclusively) the range we are searching for, then we return the value of the node.

What does that look like? We start with the top node, (34) which represents [0...7]. Parts of that interval (both 0 and 7) are outside our search interval [2...6] so we return the sum of its two children.

The node (15) represents [0...3]. Part of that is outside our search interval so we return the sum of its two children.

The node (8) represents [0...1]. This is entirely out of our search range so we return 0. The node (7) represents [2...3]. This is entirely inside our search range so we return 7.

[0...3] returns 0 + 7, which equals 7.

The node (19) represents [4...7]. Part of that is outside our search interval so we return the sum of its two children.

The node (9) represents [4...5]. This is entirely inside our search range so we return 9. The node (10) represents [6...7]. Part of that is outside our search interval so we return the sum of its two children.

The node (1) represents [6...6]. This is entirely inside our search range so we return 1. The node (9) represents [7...7]. This is entirely outside our search range so we return 0.

[6...7] returns 1 + 0, which equals 1.

[4...7] returns 9 + 1, which equals 10.

[0...7] returns 7 + 10, which equals 17. This is the same value we found above, so it's right!

This is more work than above, however it is O(log n) time. It doesn't look like it in this example because it's a very small list, but the effect is much more pronounced on larger lists. You can visit at most 4 nodes per level in the tree, which translates to 4 * log n, where n is the size of the original list. That comes out to O(log n).